Анализ статистический

Менеджеры в бизнесе часто используют статистические методы при принятии решений или анализе решаемых проблем. В данном разделе рассматриваются некоторые основные статистические методы.
Арифметическое среднее. Арифметическое среднее характеризует положение центра в распределении. Арифметическое среднее (Х) ряда значений переменной равно сумме значений данных, деленной на число значений:

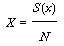
где X - арифметическое среднее;
S - сумма значений данных;
x - значение отдельной переменной;
N - число значений переменной x.
Напр., недельная продажа пяти служащих имеет следующий вид:
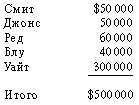5
Арифметическое среднее равно 100000 дол. и вычисляется следующим образом:

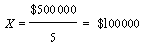
Значение арифметического среднего базируется на всех наблюдениях; на него влияют все значения переменной. При этом экстремальные значения могут входить в среднее значение со слишком большим весом. Арифметическое среднее может вычисляться алгебраическими методами.
Геометрическое среднее. Геометрическое среднее серии значений равно корню n-й степени из произведения значений. Геометрическое среднее используется при усреднении скоростей изменения или отношений, оно дает равный вес равным скоростям изменения.
Медиана. Медиана - значение среднего элемента в массиве, упорядоченном по возрастанию значений элементов. В приведенном примере еженедельного сбыта пяти служащих медианой является значение 60 тыс. дол. (сбыт Реда - Red`s sales). На медиану влияет позиция каждого элемента в серии, значение каждого элемента несущественно.
Мода. Значение переменной, к-рое реализуется наиболее часто, называется модой. В иллюстрации еженедельного сбыта пяти служащих мода равна 50 тыс. дол. (Смит и Джонс).

Скользящее среднее. Скользящее среднее для временного ряда - арифметическое или взвешенное среднее из ряда последовательных элементов ряда, где число элементов данных выбирается так, чтобы устранить сезонные эффекты или нерегулярности. Администратор по маркетингу скомпилировал данные по сбыту с января по май, отражающие сезонные изменения. Для предсказания сбыта администратор решает использовать трехмесячное скользящее среднее, чтобы устранить воздействие сезонных факторов. (Если имеются сезонные изменения, то должны использоваться данные минимум за два года.).

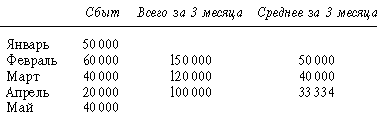
Скользящее среднее также полезно для управления описью малосерийных единиц.
Среднеквадратичное отклонение. Среднеквадратичное отклонение используется, чтобы интерпретировать изменчивость набора данных. Оно является мерой дисперсии (разброса) данных. Приблизительно 68% всех значений будет попадать в диапазон одного среднеквадратичного отклонения в обе стороны от среднего; приблизительно 95% всех значений будет попадать в диапаправления описью малосерийных единиц.
Среднеквадратичное отклонение. Среднеквадратичное отклонение используется, чтобы интерпретировать изменчивость набора данных. Оно является мерой дисперсии (разброса) данных. Приблизительно 68% всех значений будет попадать в диапазон одного среднеквадратичного отклонения в обе стороны от среднего; приблизительно 95% всех значений будет попадать в диапазон двух среднеквадратичных отклонений в обе стороны от среднего; и 99,73% всех значений будет попадать в диапазон трех среднеквадратичных отклонений в любую сторону от среднего.
Среднеквадратичная ошибка среднего. Среднеквадратичная ошибка среднего характеризует среднеквадратичное отклонение распределения значений серии. `Ошибка` относится к ошибке выборочного обследования.
Взвешенное среднее арифметическое. Взвешенное среднее используется, когда наблюдения имеют различные степени важности или частоты. Напр., показатели служащего равны 90% при шестимесячной оценке и 80% при ежегодной оценке. Администратор присваивает оценкам вес 5 и 20 соответственно. Оценка по методу взвешенного среднего должна вычисляться следующим образом:
Степень Вес
x w xw
Оценка по шести месяцам 90 5 450
Окончательная оценка 80 20 1600
Итого 25 2050
Взвешенное среднее (X) вычисляется следующим образом:
      S(xw)    2050
X =--------=----------- = 82
      N      25

См. анализ временных рядов