Индексы заработной платы

Индексы заработной платы (теоретические основы, используемые в анализе результатов обследования организаций о распределении численности работников по размерам заработной платы). В соответствии с общей теорией статистики в основу обследования положен интервальный вариационный ряд распределения численности работников по размерам заработной платы. Рядом распределения в статистике называется ряд цифровых показателей, представляющих распределение единиц совокупности по одному существенному признаку.

По своей конструкции ряд распределения состоит из двух элементов: вариантов (групп по выделенному признаку) и частот (численности групп). Вариантами в данном обследовании являются интервалы по размерам заработной платы, частотами – численность работников. Частоты, выраженные в виде относительных величин (доли единиц, процентов), называются частостями. Сумма частностей равна 1, если они выражены в долях единицы, и 100%, если они выражены в процентах. Общая схема ряда распределения такова: в совокупности, состоящей из N единиц, некоторая переменная величина x (т.е. какой- либо варьирующий признак) принимает различные значения: x1, x2, x3,……. xn . Каждое из этих значений имеет частоту f 1, f 2, f 3,……. f n . Исходя из этого, вариационный ряд распределения можно представить в виде:

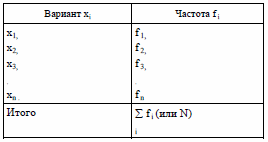
Если интервальный вариационный ряд распределения построен с равными интервалами, частоты позволяют судить о степени заполнения интервала единицами совокупности. При построении неравных интервалов на основании частот нельзя получить информацию о степени заполнения каждого интервала. В этом случае исчисляют плотность распределения. Абсолютная плотность распределения – это частота, приходящаяся на единицу длины интервала, относительная плотность распределения – частость, приходящаяся на единицу длины интервала. Для характеристики закономерностей распределения изучаемого признака рассчитываются показатели центра распределения: средняя арифметическая, мода и медиана.

По данным первичного ряда рассчитывается простая средняя арифметическая ( x ), при вычислении по данным ранжированного вариационного ряда применяется формула средней взвешенной. В отличие от средней арифметической, рассчитываемой на основе всех вариантов значений признака, мода характеризует величину варианта, занимающего определенное положение в ранжированном вариационном ряду.